Složený úrok - vzorce

Tento článek obsahuje souhrn základních vzorců finanční matematiky.
Pokud si chcete spíše spočítat úroky na vašem účtu, použijte raději naše finanční kalkulátory.

Finanční kalkulátory

Budoucí hodnota

Při odvozování základních vzorců pro výpočet složeného úročení můžeme vyjít z následujícího zadání. Mějme investiční nástroj nebo spořicí účet, který zhodnotí vklad úrokovou mírou p za jedno období. Na konci každého období se úrok připíše k jistině (kapitalizace) takže se od následujícího období také úročí. Přepokládejme, že počáteční jistina (tj. jistina na počátku prvního období) bude j₀ a na konci každého období vložíme (nebo odebereme) částku a. Bude nás zajímat jistina na konci n-tého období.

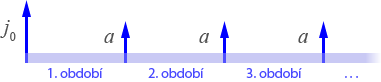
Zavedeme úročitel r = p+1, takže úrok z počáteční jistiny na konci 1. období bude roven j₀ r. Jistina na konci 1. období tedy bude

     j₁ = j₀ r + a

Podobně jistina na konci 2. období bude

     j₂ = j₀ r ² + a r + a

Obecně tedy jistina na konci n-tého období bude

     j_n = j₀ r ⁿ + a r ^n-1 + a r ^n-2 +… + a

Takže

kde j_n  je jistina na konci n-tého období, j₀  je počáteční jistina, r  je úročitel definovaný jako r = p + 1, přičemř p je úroková sazba, n  je počet období, a  je pravidelný vklad.

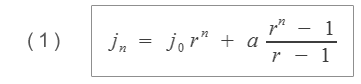
Při odvození vzorce (1) jsme předpokládali, že pravidelné vklady a jsou prováděny na konci každého období (polhůtní, neboli dekurzivní platby). Můžeme však předpokládat, že platby jsou prováděny na začátku každého období (předlhůtní, neboli anticipativní platby).

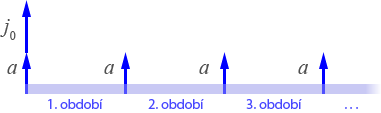
Vzorec pro výpočet jistiny na konci n-tého období pak bude

Vzorce (1) a (2) si můžete vyzkoušet v následujícím kalkulátoru. Ve vstupním poli „typ plateb“ se určuje, který ze vzorců bude použit. Další podrobnosti k těmto výpočtům najdete níže.

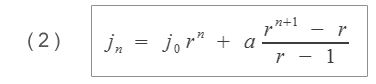
Tyto vzorce jsou také předprogramovány v Excelu, kde však mají poněkud jinou logiku používání znamének. Hodnoty počáteční jistiny a pravidelného vkladu mají obrácená znaménka než hodnoty které používáme při našem odvozením. Abychom dostali stejné výsledky, musíme jednotlivé parametry vkládat se znaménky podle následující tabulky. Názvy funkcí se liší podle jazykové mutace:

kde Typ = 0 pro polhůtní, nebo 1 pro předlhůtní vklady.

Ze vzorců (1) a (2) je možno jednoduše odvodit vzorce pro jednotlivé proměnné. Nejčastěji se používají vzorce pro výpočet pravidelné platby a a pro počet období n. Oba tyto vzorce jsou uvedeny dále.

Pravidelná platba

Z předchozích vzorců je možno snadno odvodit vzorec pro výši pravidelné platby a při polhůtních vkladech

případně pro předlhůtní vklady:

Typické použití těchto vzorců je při výpočtu splátky úvěru. Výše úvěru se vkládá jako záporná počáteční jistina, konečná jistina je nulová (požadujeme, aby úvěr byl zcela splacen). Vzorce (3) a (4) si můžete vyzkoušet v následujícím kalkulátoru. Další podrobnosti k těmto výpočtům najdete níže.

Také tyto vzorce jsou předprogramovány v Excelu, opět s odlišnou definicí znamének:

Počet období

Ze vzorce (1) lze odvodit také počet období n potřebný pro dosažení konečné jistiny j_n při počáteční jistině j₀, pravidelné platbě a a úrokové sazbě p při polhůtních platbách:

a podobně pro předlhůtní platby

Typické použití těchto vzorců je při výpočtu doby splatnosti úvěru nebo pro výpočty typu: „jak dlouho je potřeba spořit pro naspoření dané částky“. Vzorce (5) a (6) si můžete vyzkoušet v následujícím kalkulátoru. Další podrobnosti k těmto výpočtům najdete níže.

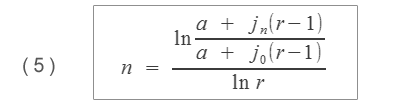
I tyto funkce mají v Excelu odlišnou definici znamének:

Poznámky k používání jednotlivých vzorců

Úroková sazba a frekvence úročení

Úroková sazba p je úroková sazba za celé období. Je obvyklé udávat úrokovou sazbu v procentech za rok, takže například úrokové sazbě 10 % p.a. odpovídá hodnota p = 0,1.

Pokud je úrokové období kratší než rok, je možno úrokovou sazbu přepočítat. Velmi často se například udává roční úroková sazba (například 3 % p.a.), ale úroky se připisují měsíčně. Pak je nutno počítat s měsíčním úrokovým obdobím, kterému bude odpovídat 1/12 roční úrokové sazby. Tedy například p = 0,03/12 = 0,0025.

Nulová úroková sazba

Při odvozování vzorců (1-6) bylo nutno předpokládat, že úroková sazba je kladné číslo. Pro hodnotu p = 0 (respektive r = 1) se ve všech vzorcích vyskytují neurčité výrazy, kdy je v čitateli i jmenovateli zlomku nula. Řešení těchto případů je sice triviální, ale například při programování či automatických výpočtech je nutno tuto eventualitu ošetřit. Kalkulátory na této straně toto ošetřené nemají (viz příklad zde).

Spoření a úvěry

Výhodou vzorců (1-6) je, že jsou univerzální pro počítání spoření i úvěrů. Peněžní toky znázorněné na začátku stránky sice odpovídají spoření s počáteční jistinou j₀, ale pokud zvolíme j₀ záporné, můžeme stejným způsobem počítat i úvěr. Zvolíme-li j₀ = -1000, můžeme pomocí kalkulátoru budoucí hodnoty spočítat výši úvěru (j_n) po deseti splátkách ve výši 100 Kč při úrokové sazbě 5 %. Dosazením dostaneme hodnotu j_n = -308,21. Znaménka v těchto vzorcích tedy odpovídají znaménkům na fiktivním bankovním účtu, na kterém by tyto obraty probíhaly.

Za vzorci jsou v textu uvedeny také názvy příslušných funkcí v Excelu. Excel má všechny tyto funkce (a řadu dalších) zabudovány. Je pouze nutno dát pozor na znaménka, protože Excel používá znaménka podle vlastní konvence (platby od klienta jsou záporné, platby které klient získává jsou kladné).

Když je počet období desetinné číslo

Z logiky věci by měl být počet období n celé číslo. Pokud však budeme počítat počet období pomocí vzorců (5-6), bude celočíselný výsledek spíše náhodou než pravidlem. Jak máme takovému výsledku rozumět?

Podobný výsledek má význam pouze při analytických výpočtech. Pro běžnou praxi těch, kdo neprovádějí kalkulace finančních derivátů může být vodítkem informace, že takový výsledek přibližně (ale opravu jen přibližně) odpovídá tomu, že počet plateb bude roven hodnotě n zaokrouhlené nahoru, přičemž poslední platba bude úměrná desetinné části hodnoty n. Pokud bude například hodnota platby a = 100 a počet období vyjde n = 5,2, pak celkový počet plateb bude 6, přičemž poslední platba bude přibližně 20 (100×0,2).

Nutno však zopakovat, že tato interpretace je pouze přibližná. Přesně platí pouze v případě, kdy je úroková sazba nulová.

Každý, kdo někdy splácel úvěr však ví, že taková situace může reálně nastat (a také nastává). Skutečnou poslední splátku je nutno počítat jiným způsobem. Tento způsob používají finanční kalkulátory na těchto stránkách.

Jak započítat poplatky?

Vzorce složeného úročení se často používají například pro výpočet částky naspořené na běžném účtu. V takovém případě je zpravidla zajimavé vědět, jak celkový výsledek ovlivní poplatky. Uvedené vzorce umožňují zahrnout do výpočtu poplatky za předpokladu, že je možno poplatky započíst proti pravidelným platbám, nebo proti počáteční jistině.

Například pokud počítáme částku naspořenou za jeden rok při úrokové sazbě 6 % p.a. při měsíční úložce 1000 Kč a měsíčnímu poplatku 10 Kč, pak za předpokladu, že úroky jsou připisovány měsíčně a vklady i poplatky jsou účtovány na konci měsíce, můžeme za měsíční úložku a dosadit 1000 – 10 = 990 Kč. Dosazením do kalkulátoru pak dostaneme, že naspořená částka j_n bude 12212.2 (při dosazení jsme roční úrokovou sazbu 6 % p.a. vydělili 12, abychom dostali sazbu za jeden měsíc).

Problém však nastane, pokud poplatky nemůžeme takto jednoduše započíst proti platbám. To je zpravidla tehdy, když jsou poplatky účtovány s jinou periodicitou než platby. V takových případech není možno uvedené vzorce použít a případ je třeba počítat jiným způsobem. Kalkulátory na těchto stránkách řadu takových výpočtů umožňují.

Související články