O vzorečcích pro jednoduché i složené úročení a jedné záludnosti

Rozdíl mezi jednoduchým a složeným úročením zná asi každý. Složené úročení je pro nás výhodnější když spoříme a naopak nevýhodné když splácíme úvěr. Ale o jak velkých číslech se bavíme? Spočítáme si konkrétní příklad a podíváme se podrobněji na vzorečky. Jak totiž uvidíme v závěru, jedná se od dva odlišné vzorce, které spolu souvisejí méně, než bychom čekali.

Jednoduché a složené úročení

Při jednoduchém úročení se úrok počítá jednoduše tak, že se počáteční jistina vynásobí úrokovou mírou za jedno období a počtem období. Celková hodnota vkladu na konci úročení tak bude

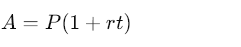
(1)

Kde

• A je konečná hodnota vkladu včetně úroků
• P je počáteční hodnota vkladu
• r je roční úroková sazba
• t je doba uložení peněz v rocích

Složené úročení je proces, kdy se úroky získané z vkladu nebo půjčky připisují k úročené jistině. Tím se jednou získané úroky opět úročí, vznikají úroky z úroků a jistina tím roste exponenciálně.

(2)

Kde

• A je konečná hodnota vkladu včetně úroků
• P je počáteční hodnota vkladu
• r je roční úroková sazba
• n je je počet úrokovacích období za rok, tedy kolikrát během roku se připíše úrok k jistině
• t je doba uložení peněz v rocích

U nás je obvyklé měsíční připisování úroků

Ve vzorečku pro složené úročení (2) jsme jako n označili četnost připisování úroků, tedy kolikrát za rok se připisují úroky k jistině. U nás je obvyklé měsíční připisování, tedy n=12. Kdyby se úroky připisovaly jen jednou ročně, bylo by n=1.

Přirozeně platí, že čím častěji se připisují úroky k jistině, tím rychleji budou úroky růst. Na první pohled ale těžko odhadneme, nakolik je významný rozdíl například mezi měsíčním a ročním úročením. Podívejme se tedy na konkrétní příklad.

Jak velké jsou rozdíly v úročení?

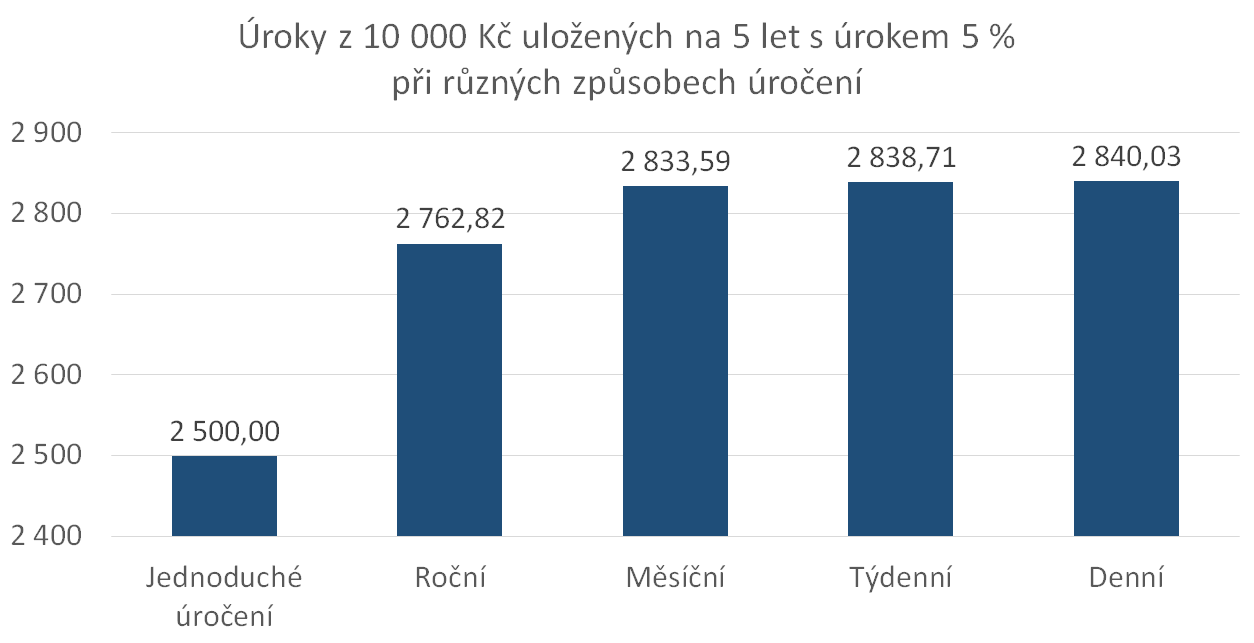
Řekněme že si uložíme 10 000 Kč na 5 let s úrokem 5 %. Jaké budou rozdíly mezi jednoduchým a složeným úročením? Podle vzorečků (1) a (2) můžeme vypočítat naspořenou částku a úroky při jednoduchém úročení i při složeném úročení s ročním, měsíčním, týdenním a denním připisování úroků. Výsledky vidíme lépe v následujícím grafu. Protože rozdíly nejsou příliš velké, je svislá osa roztažena tak, aby byly lépe vidět. Největší rozdíl je mezi jednoduchým úročením a složeným úročením s ročím připisováním úroků. Rozdíl činí 263 korun, což je více než desetina úroků získaných jednoduchým úročením. Častějším než ročním připisováním úroků vyděláme opět o něco více, ale celkový úrok roste stále pomaleji. Takže ani při denním úročení se z nás nestanou milionáři. Každého asi napadne, zda by se dalo pokračovat dál a vydělat tak ještě více. Odpověď zní: ano, dalo, ale ani zde nečekejme zázraky. I v limitním případě spojitého úročení bychom na úrocích vydělali jen 2 840,25 Kč. Na to přišel už před nějakým časem Leonhard Paul Euler a už jsem o tom jednou psal.

Vzoreček na jednoduché úročení nedostaneme(!) ze vzorečku na složené úročení

Vzorečky pro jednoduché (1) a složené úročení (2) jsou jednoduché a po kratší či delší době je  trochou přemýšlení dá dohromady každý. Přesto skrývají jednu zajímavost.

Vzorec pro složené úročení (2) obsahuje parametr n, což je počet úrokovacích období za rok. Tedy kolikrát během roku se připíše úrok k jistině. Když budeme hodnotu n zvyšovat, dostaneme se postupně na denní připisování úroků (n = 365), případně hodinové (n = 365×24), minutové atd. A již zmíněné spojité připisování úroků (n → ∞) vede k hodnotě e^rt kde e je Eulerovo číslo 2,718.

Znamená to, že když do vzorečku pro složené úročení (2) dosadíme n = 0, dostaneme vzoreček pro jednoduché úročení (1)? Na první pohled to vypadá logicky: při jednoduchém úročení se úroky k jistině nepřipisují, takže by mělo být n = 0. Dosazením do vzorce pro složený úrok dostaneme neurčitý výraz Na jednu stranu budeme mít nulu ve jmenovateli, což by znamenalo nekonečně vysokou hodnotu. Na stranu druhou ale toto nekonečno umocníme na nulu a normální (konečné) číslo umocněné na nulu je 1. který není úplně triviální. Tedy se dostáváme do velmi nebezpečné situace. Vyčíslení tohoto neurčitého výrazu je skutečně velmi pracné. Navíc všechno nasvědčuje tomu, že to nakonec nějak vyjde. Tak proč se tím trápit? Inu proto, že to nevyjde!

Když se totiž zbavíme neurčitého výrazu, dostaneme pro n → 0 vzorec A = P; jinými slovy: úrok bude nulový, čili naspořená částka bude vždy stejná jako částka vložená. Nedostaneme žádné úroky, bez ohledu na úrokovou sazbu, bez ohledu na dobu spoření. Proč?

Zádrhel spočívá ve způsobu, jakým se odvozuje vzoreček pro výpočet složeného úročení (2). V něm se vychází z předpokladu, že během jednoho období (roku) se úrok alespoň jednou připíše k jistině. To je vcelku rozumný předpoklad. Problém je, že na tento předpoklad velmi snadno zapomeneme a u výsledného vzorečku se obvykle neuvádí varování, pro jaké hodnoty n jej můžeme používat. Není problém připisovat úroky častěji a častěji. Měsíčně, denně, každou vteřinu, nebo ještě častěji. Ale jak si představit připisování úroků například 0,5krát za rok? To nedává smysl.

Takže dosazením n = 0 nedostaneme vzorec pro jednoduché úročení, ale vzorec pro žádné (nulové) úročení. Úrok se nepřipisuje, žádný úrok není, a tedy A = P.

A úplně na závěr ještě jedna drobnost: Vzoreček pro složený úrok nefunguje přesně ani tehdy, když počítáme úrok za necelý počet let. Nebo přesněji: když součin n×t není celé číslo. Vzoreček dá v takovém případě výsledek který je téměř správný, ale správný není. Příčina tkví opět ve způsobu odvození. Zjednodušeně řečeno: úroky (a tedy i zůstatek) rostou s časem lineárně, pouze v okamžicích kdy se připisují k jistině se mění konstanta úměrnosti (směrnice). Ovšem vzoreček (2) je typická exponenciální funkce, která se s realitou sejde právě tehdy, když n×t je celé číslo. Ale o tom zase někdy jindy.

Autor: Petr Kielar