Jak co nejlépe spočítat RPSN
RPSN je ze zákona výsledek řešení rovnice
Jak se vlastně RPSN počítá? V příloze zákona o spotřebitelském úvěru najdeme, že RPSN je řešením následující rovnice: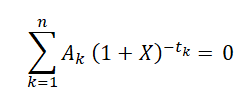
Ak jsou jednotlivé peněžní toky, tedy čerpání a splátky úvěru a
tk je časový interval v rocích a zlomcích roku mezi datem prvního čerpání a datem k-tého peněžního toku (čerpání nebo splátky)
Řešení této rovnice není nic snadného ani pro zkušeného počtáře, zpravidla je nezbytné řešit rovnici numericky, pomocí počítače. Jen v některých případech, kdy má úvěr jen několik málo splátek, umíme rovnici vyřešit. Podívejme se pro začátek na jeden takový jednoduchý příklad, který si může spočítat každý.
Jednoduchý úvěr se dvěma splátkami
Vezměme si úvěr ve výši 100 Kč, který je splacen dvěma ročními splátkami po 52 Kč. Zadání může vypadat například takto:
Úvěr ve výši 100 Kč je splacen dvěma ročními splátkami po 52 Kč.
| 1. května 2019 | Výplata úvěru | -100 Kč |
| 1. května 2020 | Splátka | 52 Kč |
| 1. května 2021 | Splátka | 52 Kč |
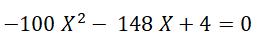
RPSN2 = -150,655 %
RPSN z pohledu matematiky
Při bližším zkoumání zjistíme, že rovnice pro výpočet RPSN vede na úlohu hledání kořene mnohočlenu n-tého stupně. To je úloha matematikům velmi dobře známá a ví se o ní mnoho věcí. Obecně vypadá rovnice takto:
Komplexních kořenů je n – včetně těch násobných
V předchozí větě jsem úmyslně použil plurálu. Z matematiky totiž víme, že mnohočlen stupně n má n kořenů, přičemž tyto kořeny mohou být násobné a mohou to být komplexní čísla. Pokud si nemůžete vzpomenout, pak nejznámější komplexní číslo je odmocnina z -1 a značí se i. A tady přicházejí první obtíže. Zákon sice hovoří jasně (RPSN je řešením předepsané rovnice), ale přiznám se, že kdybych jako klient našel v úvěrové smlouvě v kolonce RPSN seznam několika desítek komplexních čísel, nebyl bych tím potěšen. Formálně bychom sice mohli počítat i s komplexními čísly, ale počítat u úvěru jeho reálnou a imaginární část nedává dobrý smysl. Vycházejme tedy z předpokladu, že RPSN má pomáhat klientům při výběru úvěru a zaveďme si pravidlo, že pokud vyjde RPSN jako komplexní číslo, nebudeme k němu přihlížet.Při výpočtu RPSN se omezíme na řešení v oboru reálných čísel.
Co se záporným RPSN?
Pokud se omezíme pouze řešení v oboru reálných čísel, narazíme na další problém. Jak jsme viděli již v Příkladu 1, může hodnota RPSN vyjít záporná. Co s tím? Můžeme záporná řešení prostě škrtnout?Většinou ano, ale musíme být opatrní. Zatímco komplexní hodnota RPSN vede k absurdním důsledkům, záporná hodnota RPSN by mohla být za určitých podmínek zcela na místě. To se týká případů, kdy by celkový součet splátek úvěru byl nižší, než výše poskytnutého úvěru. Takový úvěr by byl pro poskytovatele nevýhodný (ztrátový), nikoli však nemožný. Dává tedy dobrý smysl zavést následující pravidlo:
Při výpočtu RPSN se omezíme na řešení, která mají stejné znaménko, jako rozdíl celkových splátek úvěru a výše úvěru.
Stále zbývá mnoho řešení
Zákon neříká nic o tom, kolik možných řešení má rovnice pro výpočet RPSN. Pouze tiše (a mylně) předpokládá, že je řešení pouze jedno. Dvě výše uvedená pravidla nás zbaví komplexních i záporných čísel. To je ale bohužel málo. Stále se může stát, že dostaneme více než jedno řešení.Když zalovíme v paměti, vzpomeneme si na jednu poučku která říká: mnohočlen stupně n má nejvýše n reálných kořenů. Přitom stupeň polynomu n je zpravidla roven počtu splátek. Naštěstí existuje Dascartesova věta, které říká:
Podívejme se na následující příklad: jednoduchý úvěr, který je jednorázově vyčerpán a poté následují již jen splátky. To je nejjednodušší a zřejmě i nejběžnější situace a znaménko peněžních toků se zde mění právě jednou.
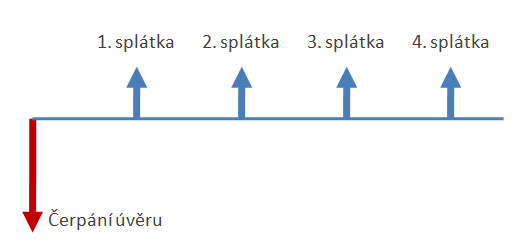
Ne každý úvěr je jednoduchý
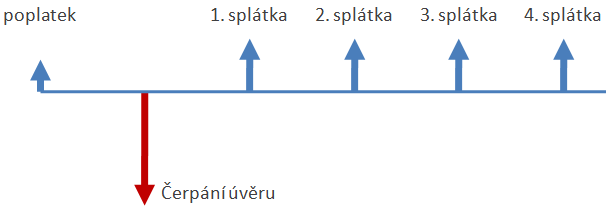
Descartesova věta nám na jedné straně zajistí, že jednoduché úvěry mají právě jedno RPSN, na straně druhé nám však napovídá, že u jiných, složitějších úvěrů, může být řešení více. Co se stane, když před prvním čerpáním bude klient povinen uhradit nějakou platbu? Zde se znaménka peněžních toků změní dvakrát, což podle Descartesovy věty znamená, že bychom pro RPSN mohli dostat dvě řešení. To nezní příliš dobře, ale než budeme přemýšlet co s tím, podívejme se na konkrétní příklad.Řekněme, že máme úvěr ve výši 1 mil. Kč, který splácíme měsíčními splátkami 10 000 Kč po dobu 10 let. Úvěr však musíme zajistit zástavním právem k nemovitosti a za odhad ceny nemovitosti musíme zaplatit 5000 Kč, a to jeden měsíc před prvním čerpáním úvěru. Tento příklad již z hlavy nespočítáme. Můžeme však použít kalkulátor RSPN, který nám vrátí dvě možná řešení: 3,912 % a 4,094×1029 %
Úvěr ve výši 1 mil. Kč je splácen měsíčními splátkami ve výši 10 000 Kč po dobu 10 let. Navíc je klient povinen měsíc před poskytnutím úvěru zaplatit poplatek za ohodnocení nemovitosti ve výši 5 000 Kč.
| 1. května 2019 | Poplatek | 5 000 Kč |
| 1. června 2019 | Výplata úvěru | -1 000 000 Kč |
| 1. července 2019 | 1. splátka | 10 000 Kč |
| 1. srpna 2019 | 2. splátka | 10 000 Kč |
| ⋮ | ⋮ | ⋮ |
| 1. června 2029 | Poslední splátka | 10 000 Kč |
RPSN1 = 3,912 %
RPSN2 = 4,094 ×1029 %
Předpokládejme konstrukci úvěru, při které klient nejprve zaplatí úroky (4 990 Kč), po třech měsících obdrží jistinu (20 000 Kč) a tu za další tři měsíce vrátí. Kalkulátor RPSN nám opět vrátí dva výsledky, a to 1 243 % a 1 821 %.
Poskytnutí úvěru je podmíněno splacením úroků předem. Úvěr ve výši 20 000 Kč je vyplacen 3 měsíce poté, co klient zaplatí úroky ve výši 4990 Kč. Splátka jistiny následuje 3 měsíce po čerpání úvěru.
| 1. května 2019 | Splátka úroků | 4 990 Kč |
| 1. srpna 2019 | Výplata úvěru | -20 000 Kč |
| 1. listopadu 2019 | Splátka jistiny | 20 000 Kč |
RPSN1 = 1 243,13 %
RPSN2 = 1 821,32 %
Z Descartesovy věty víme, že problém nám způsobuje ona první platba úroků předem. Představme si tedy, že je první platba úroků nulová. Dostaneme jednoduchý případ úvěru (jedna výplata, jedna splátka), kde se znaménko peněžních toků změní jednou, což znamená právě jedno řešení. A protože výše splátky je přesně rovna výši úvěru, je dokonce zřejmé, že řešením bude RPSN = 0 %.
Představme si nyní, že první platbu zvýšíme z nuly o nepatrnou malou částku. V tom okamžiku vzniknou dvě řešení, přičemž jedno bude blízké nule a druhé bude (naštěstí) hodně vysoké.
Když pak budeme výši první platby úroků zvyšovat, budou se obě řešení k sobě přibližovat. Dobře je to vidět v následující tabulce:
| Výše úroků | RPSN1 | RPSN2 |
| 0 Kč | 0 | neexistuje |
| 1 Kč | 0,02 % | 1,598 ×1019 % |
| 10 Kč | 0,20 % | 1,60 ×1013 % |
| 100 Kč | 2,04 % | 1,57 ×1011 % |
| 1 000 Kč | 24,22 % | 1,29 ×107 % |
| 2 000 Kč | 61,33 % | 619 738,69 % |
| 4000 Kč | 264,75 % | 17 035,26 % |
| 4 500 Kč | 433,08 % | 7 219,38 % |
| 4 990 Kč | 1 243,13 % | 1 821,32 % |
Tímto postupem můžeme dojít k závěru, že ta správná hodnota je RPSN1 = 1 243 %, protože se k ní dostaneme postupným spojitým zvyšováním první platby (úroků) z nuly až na plnou částku 4 990 Kč. V tomto případě tedy neobstojí často slýchané doporučení „v případě nejistoty použijte vyšší RPSN“. Zde je naopak správnějším výsledkem menší hodnota RPSN. Tento postup můžeme zobecnit do následujícího pravidla:
Pokud i po aplikaci Pravidla 1 a Pravidla 2 zbude více řešení, lze nalézt pomocí Descartesovy věty peněžní tok, který způsobuje existenci více řešení. Správné řešení je takové, které má vlastní limitu když tento peněžní tok jde k nule.
Co říci závěrem
Čím déle se výpočtem RPSN zabývám, tím méně se mi líbí. Nepochybně je to nejlepší způsob, jak do úrokové sazby zahrnout kromě úroků také různě skrývané poplatky. Nevýhodou však je, že u jiných než běžných úvěrů (tj. nejprve výplata a po ní následují splátky) mohou vzniknout obtížně řešitelné situace. Z pohledu klienta – spotřebitele je zde ještě jedna nevýhoda: většina lidí RPSN upřímně nechápe. Podle průzkumu ministerstva financí z roku 2015 (novější jsem nenašel) pouze 40 % dotázaných si myslí že ví, co znamená RPSN. A z těch co si to myslí, se přibližně třetina mýlí. Podle MF má skutečnou znalost RPSN jen 21 % dospělých.Běžný spotřebitel si poradí po svém – ignoruje RPSN a řídí se zdravým rozumem, který vede k otázce „Kolik to všechno dohromady stojí?“. Naštěstí se ukazuje, že celková výše splátek je dobré kriterium pro výběr úvěru. Samozřejmě za předpokladu, že zahrnuje skutečně všechny náklady s úvěrem spojené – tedy včetně poplatků a případných dalších více či méně skrytých plateb.
Poskytovatelé úvěrů však mají nezáviděníhodnou povinnost vypořádat se s matematickou úlohou, která není tak úplně jednoduchá. Střetává se zde snaha zákonodárce definovat RPSN co nejpřesněji a nejobecněji pro všechny možné úvěrové produkty na straně jedné, a marnost takového úsilí na straně druhé. Je pravděpodobné (nikoli však jisté), že ve sporných případech by bylo vhodné při výpočtu postupovat tak, aby výsledná hodnota RPSN co nejlépe odrážela cenu zapůjčovaných peněz. K tomu mohou sloužit pravidla, načrtnutá v tomto článku. Tedy
- Pravidlo 1: Zanedbat komplexní řešení.
- Pravidlo 2: Zanedbat záporná řešení (pokud je celková výše splátek vyšší než výše úvěru).
- Pravidlo 3: V případě existence více kladných reálných řešení vybrat to řešení, které má vlastní limitu pokud vybraný kritický peněžní tok jde k nule.
Autor: Petr Kielar