Jak nahlédnout do budoucnosti našich peněz

Spoření používá v nějaké podobě snad každý. Často se proto setkáme s úkolem spočítat, kolik budeme mít naspořeno za rok, za dva, nebo za deset let. Někdy to spočítáme z hlavy, jindy použijeme kalkulačku. Ve složitějších případech sáhneme k Excelu, který nám může ušetřit hodně práce. Víte ale, jaké záludnosti v sobě skrývá a na co si musíme dát pozor? V tomto článku si rozebereme jak funguje spoření, jak se počítají úroky a proč Excel může v některých případech poskytovat odlišné výsledky.

Jak vypadá spoření

Než se ponoříme do světa finanční matematiky a Excelu, pojďme se podívat na klasický způsob spoření, který používají banky. Na začátku období (může to být měsíc nebo rok), uložíme na účet určitou částku. Banka nám následně na konci období spočítá úroky a připíše je k našemu původnímu vkladu.

Uveďme si to na příkladu: Uložíme 20 Kč na účet s úrokovou sazbou 10 %. Na konci prvního období budeme mít na účtu 22 Kč. Náš původní vklad se zvýšil o úrok 20 Kč × 10 % = 2 Kč.

Teď ještě přidáme pravidelné vklady, které budeme na účet posílat na konci každého období. Když bude pravidelný vklad 10 Kč, budeme mít na konci prvního období celkem 32 Kč.

Stejným způsobem můžeme vypočítat naspořenou částku na konci druhého období. Protože se nám bude úročit zůstatek z konce prvního období, bude úrok za druhé období 32 Kč × 10 % = 3,20 Kč. Společně s dalším pravidelným vkladem (10 Kč) tedy budeme mít na konci druhého období 32 Kč + 3,20 Kč + 10 Kč = 45,20 Kč.

Nastupuje finanční matematika

Tímto způsobem bychom dokázali spočítat naspořenou částku v libovolném budoucím okamžiku. Potřebovali bychom jen hodně času a trpělivosti. Práci si ale můžeme usnadnit pomocí vzorců finanční matematiky. Snadno si můžeme odvodit, že zůstatek na konci libovolného období spočítáme rychleji pomocí vzorce: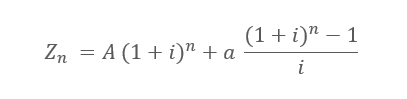 kde A je počáteční vklad, a je pravidelná úložka, i úroková sazba a n je počet období. Jako každý vzoreček, i tento má tu nevýhodu, že se špatně pamatuje. Naštěstí můžeme použít Excel a jeho funkci BUDHODNOTA V českém prostředí se funkce jmenuje BUDHODNOTA, v anglickém je označena jako FV (Future Value). , která tento vzorec obsahuje. Stačí jenom vložit správné parametry:

BUDHODNOTA( i; n; -a; -A)

Úložky a a A vkládáme se záporným znaménkem, protože Excel je nastaven tak, že peníze které vydáváme (posíláme na účet) mají mít záporné znaménko. Když budeme chtít spočítat naspořenou částku na konci prvního období, spočítáme BUDHODNOTA(10%; 1; -10; -20) a skutečně dostaneme 32 Kč. Zdá se tedy, že vše funguje podle našeho očekávání.

Zádrhel v polovině období

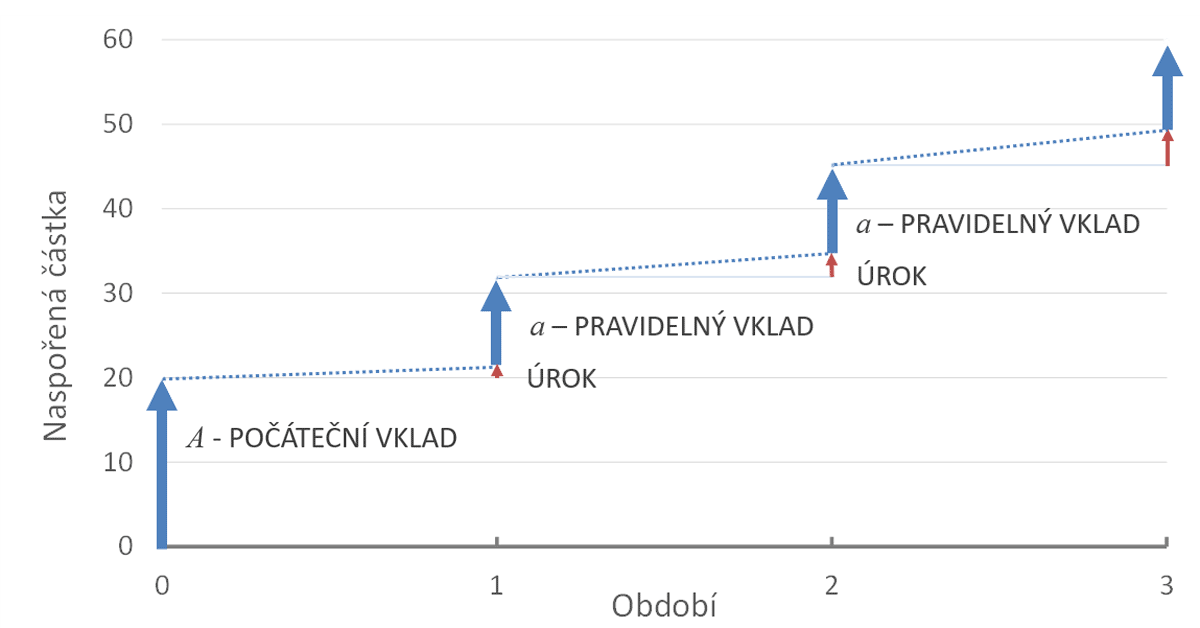
Představme si ale, že chcete znát stav účtu nikoli na konci, ale třeba v polovině prvního období. Spočítáme tedy BUDHODNOTA(10%; 1/2; -10; -20) a dostaneme 25,86 Kč. To ale neodpovídá tomu co bychom očekávali! Na začátku prvního období jsme vložili 20 Kč ke kterým přibyly nějaké úroky, ale celkem to nemůže být 25,86 Kč. Úroky za celé první období jsou 2 Kč, takže za polovinu období to bude jen 1 Kč. Na účtu bychom tedy měli mít 20 Kč plus úroky 1 Kč. To je podstatně méně, než nám ukazuje výpočet. Jak je to možné?

Vklady v bance se úročí tak, jak je nakresleno na obrázku. V průběhu období se uložené peníze zvyšují u úroky, ty se ale na účtu neobjeví. Banka je připíše na účet až na konci období, tedy na konci roku nebo poslední den v měsíci. Ve stejném okamžiku se vklad zvýší o pravidelnou úložku a. Naspořená částka se tedy skokem zvýší o úroky a pravidelný vklad.

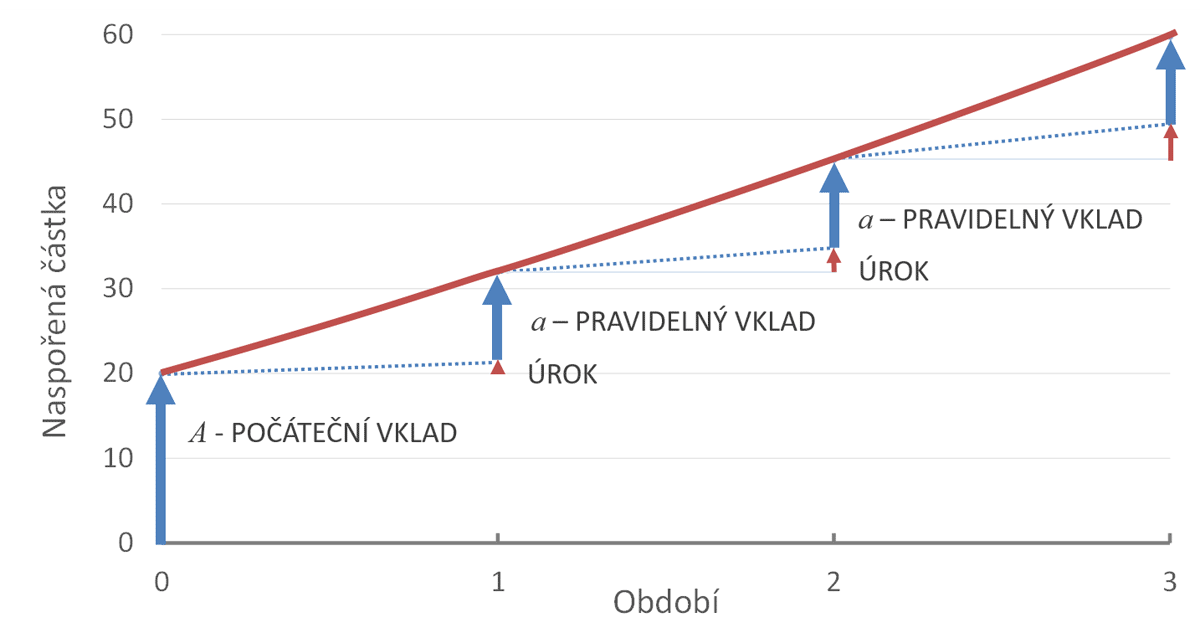
Když si nakreslíme funkci BUDHODNOTA, dostaneme trochu jiný obrázek. Naspořená částka se mění spojitě, nejsou tam žádné skoky.Na konci období, tedy když je počet období n celé číslo, odpovídá BUDHODNOTA tomu co očekáváme při úročení na bankovním účtu. Kdykoli jindy je tam ale rozdíl.

Jak je to tedy správně?

Dříve než se pustíme do počítání je potřeba si ujasnit, co vlastně počítáme. Vzoreček pro výpočet budoucí hodnoty, stejně jako funkce BUDHODNOTA v Excelu počítá spojitou závislost zůstatku na čase. Je to abstrakce, která odpovídá reálnému stavu bankovního účtu jen tehdy, když je počet období n celé číslo. V řadě případů to nevadí, nebo je takové chování dokonce žádoucí.

Problém nastane, když funkci finanční matematiky použijeme k výpočtu zůstatku na účtu. Což je však situace, se kterou se běžný střadatel setká poměrně často. Co dělat v takovém případě?

Můžeme použít postup vysvětlený na začátku: počítat postupně zůstatky v jednotlivých obdobích, dokud se nedostaneme k cíli. Ale můžeme použít i zkratku: využijeme toho, že funkce BUDHODNOTA funguje bezproblémově na konci období, kdy n je celé číslo. Takto můžeme jednoduše spočítat zůstatek na konci nejbližšího období a zbývající část dopočítat „ručně“.

Řekněme že nás zajímá zůstatek v polovině třetího období. Pomocí funkce BUDHODNOTA spočítáme zůstatek na konci druhého období a přičteme úrok za polovinu třetího období.

• Zůstatek na konci druhého období je BUDHODNOTA(10%; 2; -10; -20) = 45,20 Kč.
• Úrok za polovinu třetího období spočítáme jako 45,20 Kč × 10 % / 2 = 2,26 Kč.
• Celkem tedy budeme mít na účtu 45,20 Kč + 2,26 Kč = 47,46 Kč.

Autor: Petr Kielar