O síle složeného úročení a nedostižné exponenciále

Složené úročení aneb budoucí hodnota
Princip složeného úročení je jednoduchý. Když si uložíme jednu korunu na účet s 10% úrokem, za rok nám vydělá 1×10 % = 0,1 Kč. Tento úrok se na konci roku připíše k zůstatku, takže ve druhém roce se již nebude úročit jen jedna koruna, ale (1 + 1×10 %) = 1,1 Kč. Na konci druhého roku tedy bude na účtu (1 + 1×10 %)2. Po n letech bude na účtu naspořena částka(1 + 10 %) n = 1,1n.
Finanční matematika popisuje tento vztah jako budoucí hodnotu FV, kdej je částka vložená na počátku,
n je počet období, a
i úroková míra.
FV = j (1 + i) n.
Důležité je, že budoucí hodnotu peněz určuje exponenciální funkce. A o ní je známo, že roste hodně, hodně rychle. A ukážeme si, jak hodně dokáže růst.
Jednoduché úročení proti úročení složenému
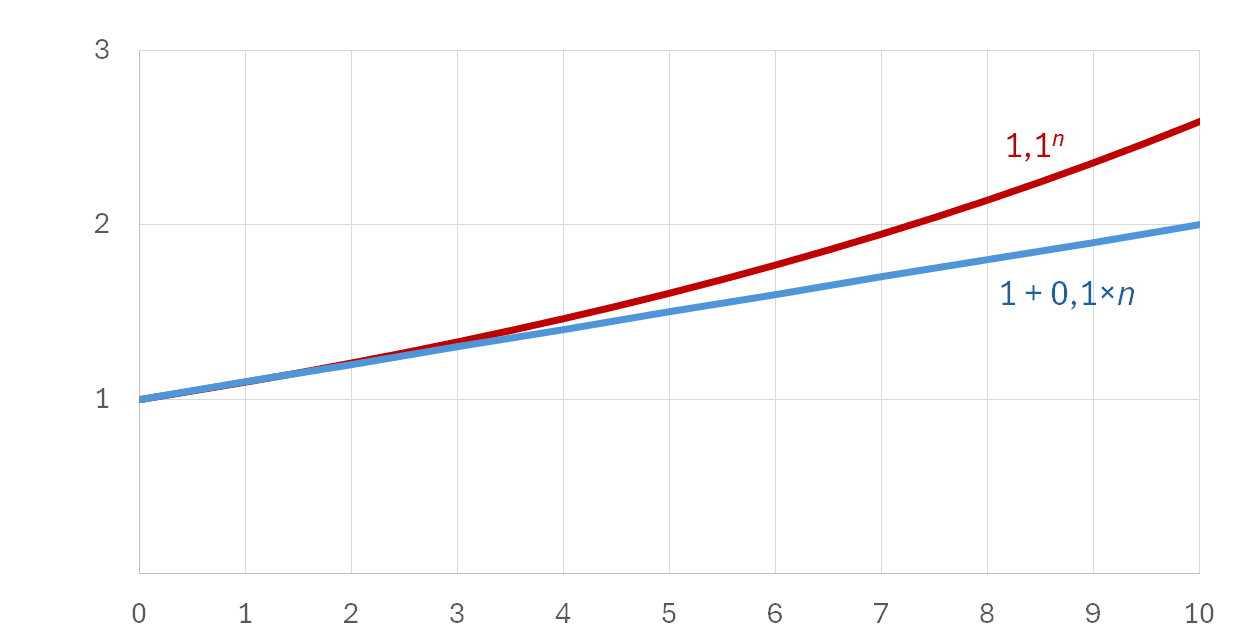
Začněme tím nejjednodušším. Snad každý ví, že složené úročení dává vyšší úrok, než úročení jednoduché. Velí tak i selský rozum – když se budou úročit i úroky, bude úrok vyšší. Při jednoduchém úročení bude po uplynutí n období naspořená částka1 + 1 × 10 % × n.
Jednoduchý úrok to má těžké, zkusme mu proto pomoci tím, že zvýšíme úrokovou míru na dvojnásobek. Je to sice neférový doping, ale podívejme se, co se stane. Naspořená částka bude růst dvojnásobnou rychlostí, tedy1 + 1 × 20 % × n.
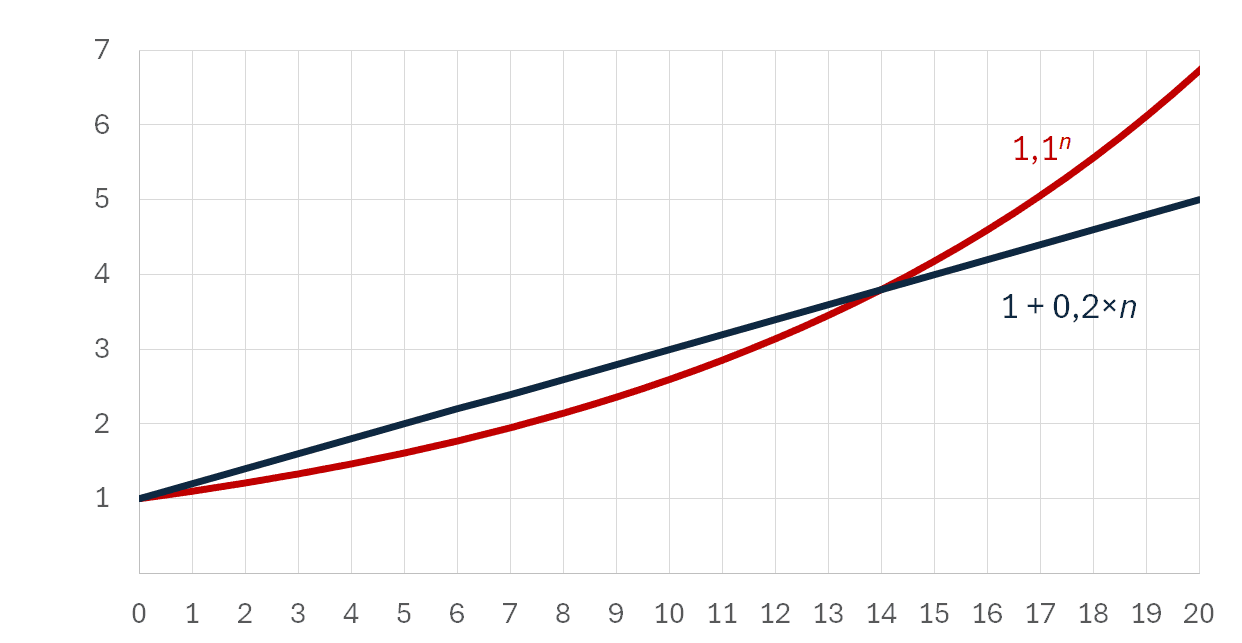
Naspořená částka skutečně poroste rychleji a během prvních deseti let bude přesvědčivě vyšší, než složený úrok při poloviční (desetiprocentní) úrokové míře. Počkejme ale několik let. Ve 14. roce složený úrok (exponenciála) dohoní jednoduchý úrok (lineární funkci) a dále bude jen navyšovat svůj náskok. Asi netřeba říkat, že ani s dalším zvyšováním úrokové míry bychom nepochodili. Pro libovolně vysokou úrokovou míru stačí jen nějakou dobu počkat a exponenciála (složený úrok) ji předhoní. Je to „jen“ otázkou času. Můžeme ale zkusit něco jiného.
Co druhá mocnina?
Nyní se zcela oddělíme od reálného světa tím, že si vymyslíme jiný rychlejší úrok, který se pokusíme pokořit složené úročení. Při jednoduchém úročení úrok roste lineárně s časem. Tedy za 1. je 10 % jistiny, za 2. rok přibude dalších 10 % takže celkový úrok bude 10 % + 10 % = 20 % a tak dále. Úrok za n období je 10 % × n. Co kdyby úrok rostl se čtvercem času? Tedy s druhou mocninou počtu období?Úrok za 1. období by zůstal stejný, tedy 10 %. Ale úrok za první dvě období by nebyl 10 % × 2 = 20 %, ale 10 % × 22 = 10 % × 4 = 40 %. A za první tři období dokonce 10 % × 32 = 10 % × 9 = 90 % a tak dále. Obecně by byla naspořená částka za prvních n období rovna
1 + 10 % × n2.
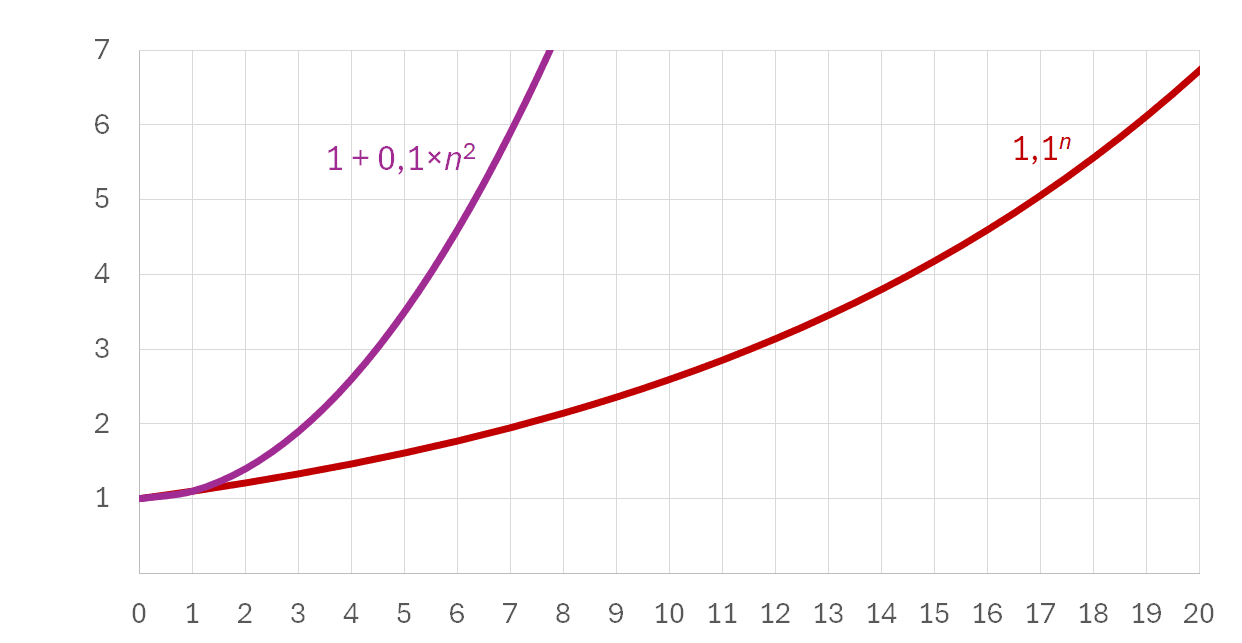
Jistina by tedy rostla s druhou mocninou počtu období. To vypadá jako dosti rychlý růst, a v grafu to i vidíme. I přesto, že „kvadratický“ úrok roste podstatně rychleji než obyčejné jednoduché úročení, stejně složené úročení nepokoří. Stačí počkat 64 let. Po 64 letech začne složené úročení dávat vyšší výnos. Bylo by jistě možné zkusit třetí nebo čtvrtou mocninu, ale brzy si ukážeme, že ani to by nepomohlo. Exponenciála (tedy složené úročení) v dostatečně dlouhém časovém horizontu dá vyšší úrok.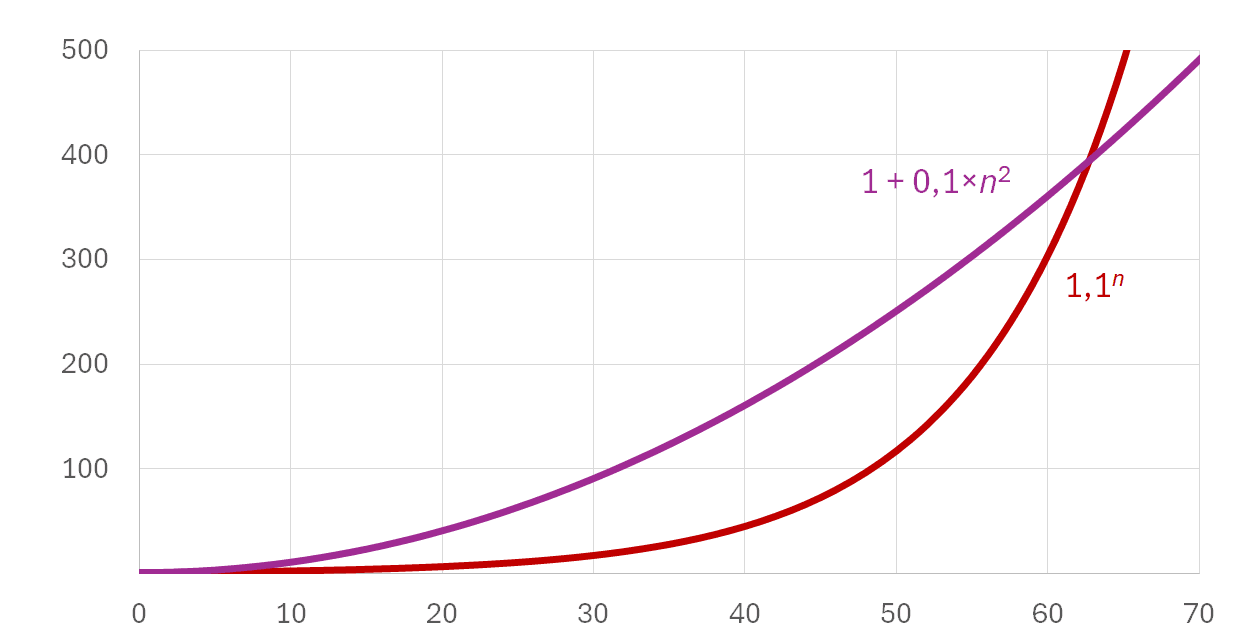
Návrat do školních škamen
Tím se dostáváme k podstatě věci. Dá se totiž matematicky dokázat, že složený úrok (exponenciála) v dlouhodobém horizontu roste rychleji, než úrok vyjádřený mocninou libovolného (konečného) řádu. Tedy i kdyby byl úrok vyjádřen jako 10 % × n3333, vždy bude dlouhodobě méně výhodný, než složený úrok. I když v některých případech bude tato „dlouhodobost“ skutečně hodně dlouhá.Matematicky se dá tato myšlenka vyjádřit tak, že vytvoříme zlomek. Ve jmenovateli bude jistina při složeném úročení po uplynutí n období, tedy (1 + 10 %)n. Do čitatele dáme jistinu při mocninném úročení, kde úrok po n obdobích bude 10 % × nk, kde k je libovolné číslo. Pro jednoduché úročení je k = 1, pro kvadratické úročení, které jsme zkoušeli výše, je k = 2. Ale ukážeme, že úvaha platí pro libovolně vysoké k.
Budeme zkoumat hodnotu tohoto zlomku pro hodně dlouhé období, tedy když n půjde do nekonečna. Ukážeme, že pro dostatečně velký počet období bude hodnota zlomku klesat k nule. To znamená, že hodnota jmenovatele (složený úrok) bude nesrovnatelně vyšší, než čitatel (mocninný úrok):
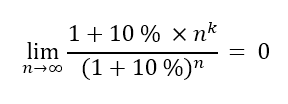
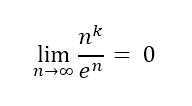
To, že zmíněny zlomek konverguje k nule neznamená pouze, že exponenciála je v nekonečnu větší, než libovolná mocnina. Znamená, že je nekonečně větší! Když se na to podíváme z jiné stránky: když budeme spořit nekonečně dlouho, naspoříme si i při jednoduchém úročení nekonečně mnoho peněz. V čitateli tedy bude nekonečno. Ale v jmenovateli máme částku naspořenou složeným úročením, a ta bude TAK velká, že celý zlomek dá nulu Zjednodušeně se dá říci, že ve jmenovateli bude větší nekonečno, než v čitateli. . A to i v případě, že z jednoduchého úročení uděláme mocninné úročení, kdy úrok bude úměrný libovolné mocnině počtu období.
Záhada průměrně naspořené částky a její souvislost se stářím kolektivu
Autor: stavebky.cz


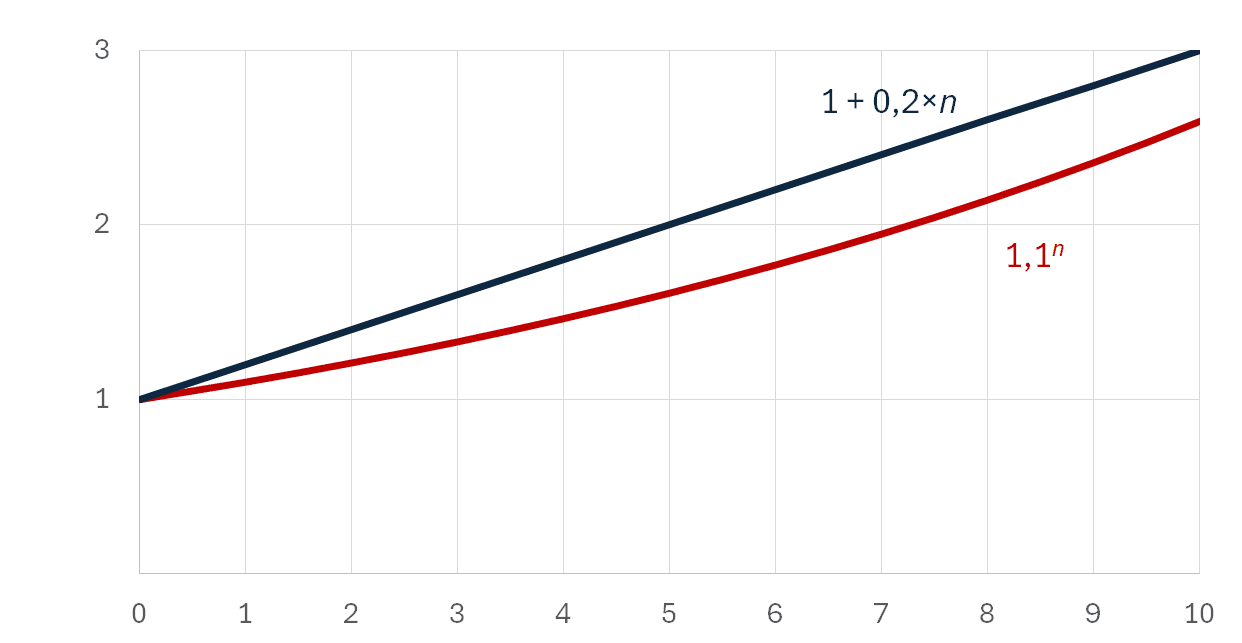








Komentáře (0) ke článku
O síle složeného úročení a nedostižné exponenciále